In some of my other posts, I’ve explained what’s meant by “criticality” with regards to nuclear reactors and that it’s not necessarily a bad thing. But what I didn’t really get into are some of the nuances of criticality – what’s meant by the terms critical mass and critical geometry, the difference between criticality in a nuclear reactor versus a nuclear weapon, and so forth. So this seems like a good time to take a deeper look at criticality – starting with a quick refresher on the basics.
To start with, the term “criticality” is, I guess you could say, non-judgmental. By that, I mean that the term is neither inherently good nor bad – it’s simply descriptive. When a uranium atom fissions it emits two or three neutrons; if one of those neutrons (on average) goes on to cause a second fission then the reaction is said to be “critical.” If more than one fission occurs then the reaction is super-critical; less than one fission means that the reaction is subcritical.
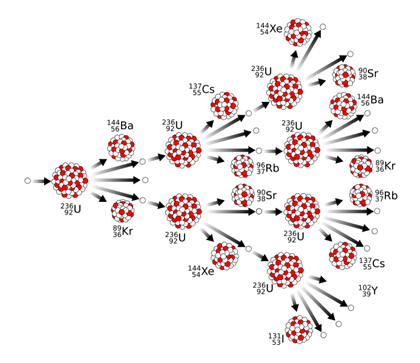
A critical chain reaction
In the setting of a nuclear reactor, supercriticality means that the reactor is starting up (increasing power), subcriticality means that the reactor’s shutting down (or reducing power), and criticality is its normal operating state of being. A reactor can be critical and producing barely enough energy to heat a cup of coffee…or to light up a city, or anything in between. When we were starting up the reactor on the submarine I was stationed on the announcement “the reactor is critical” was met with a yawn (if it was an early-morning startup) and a notation in our logs.
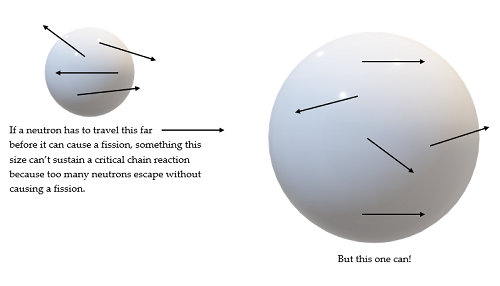
Now – say, to pick a number, that a neutron has to travel an average distance of one inch before it can be absorbed by a second uranium atom, causing it to fission. If that’s the case, is it possible for a ball of uranium an inch in diameter to sustain a fission? Well…no – because most of the neutrons will be formed less than an inch from the surface and many of those neutrons will escape from the ball of uranium first. In order for a ball of uranium to achieve criticality, it has to be large enough that most of the neutrons emitted will remain within the uranium so they can go on to cause a fission. For nuclear weapons-grade U-235 that turns out to be a little bigger than the size of a softball and weighs a little over 100 pounds – this is a critical mass for U-235 as a bare sphere of uranium metal. Changing the density, the chemical composition, and the uranium enrichment will change the critical mass, as well as surrounding the sphere with materials that will reflect escaping neutrons back into the sphere.
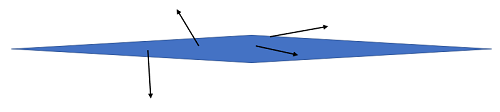
If the fissionable material is in a flat plane, most of the neutrons will escape without causing a fission, while in a more compact shape (a sphere, for example) like the one shown above these same neutrons would be able to be absorbed by another uranium atom, causing the fission reaction to continue.
OK – so now picture that sphere of uranium melted down into a paper-thin flat sheet. Will this achieve criticality? Well…no – because the only way a neutron can find another uranium atom in which to cause a fission is to be emitted in the plane of the sheet – the great majority will escape. But it’s also easy to visualize slowly crumpling this thin sheet of uranium until, eventually, most of the neutrons will remain within the uranium – this is a critical geometry. We need both a critical mass and a critical geometry to achieve criticality. In fact, an important aspect of nuclear criticality safety is making sure that one cannot achieve both of these at the same time.
So the first shape would weigh less than a critical mass and the second will weigh more.
And this brings up an interesting couple of questions – why is it that criticality in a reactor is not very thrilling, but criticality in a nuclear weapon is bad? And why is it that we need to add water to a nuclear reactor to achieve criticality, but not in nuclear weapons – especially if neutrons need to be moving slowly to cause a fission?
The answer to both of these questions begins with the amount of U-235 – the enrichment – of the uranium in question. In a nuclear reactor, there is far less U-235 and far more U-238 than there is in a nuclear weapon. This means that there are fewer “target atoms” in a given volume of reactor fuel (where 3-6% of the atoms are U-235) than there are in the same volume of weapons-grade uranium (in which over 90% of the atoms are U-235). It turns out that U-235 will fission if it’s struck with a fast neutron – it’s just not as likely as when the neutrons are moving at a more sedate pace. On top of that, fission caused by fast neutrons produces up to twice as many neutrons compared to atoms that are split by slower-moving neutrons, which also helps to make up for the lower efficiency of fast neutrons in causing fission to occur.
In a reactor, this means that we need to give the neutrons the best chance possible to cause a fission, and this means slowing them down with a moderator like water. In weapons-grade uranium, on the other hand, there are so many U-235 atoms that even fast neutrons are likely to be able to cause a fission. And since the neutrons in a nuclear weapon don’t need to be moderated and don’t travel as far, they can cause fission more quickly than in a reactor – this, the presence of control rods in a reactor to help absorb excess neutrons, and one other thing I’ll get to in just a moment is why the chain reaction in a nuclear reactor is controlled and that in a nuclear weapon is not.
The final piece of the criticality puzzle has to do with the two types of neutrons emitted during fission – prompt and delayed neutrons. Prompt neutrons are emitted immediately when the atom is split and they go on to cause fission fairly quickly as well (within nano- or microseconds), but there are neutrons that don’t emerge for seconds or minutes – these are the delayed neutrons. In a nuclear reactor, which operates for days, weeks, or even months at a time, delayed neutrons contribute to the neutron population in the reactor core, so they’re factored in with the prompt neutrons when designing a nuclear reactor core. It makes sense – a reactor startup can take several hours, so delayed neutrons can even play a role in controlling the reactor from the time the first control rods are pulled until they are inserted to shut it down. And, in fact, were it not for these delayed neutrons it would be impossible for a person to control the reactor – and would be very difficult even for electronic systems. Were it not for delayed neutrons we would likely not have nuclear reactors. In a nuclear weapon, by comparison, there’s not enough time for delayed neutrons to make an appearance – nuclear weapons are critical (actually supercritical) on prompt neutrons alone.
There are a lot more aspects of nuclear criticality – criticality safety comes to mind, for example – but they start to get a bit more complicated so this seems like a good place to stop for the moment. So let’s do a quick rehash and then we can call it a day!
- Criticality simply means that the number of fissions is staying constant over time – that one neutron from a fission goes on to cause another fission.
- There is a minimum amount of fissile material that will sustain a critical chain reaction – this is called the critical mass.
- It’s also important for the mass of material to be in a configuration in which most of the neutrons have a chance of causing a fission – this is the critical geometry – without both a critical mass and a critical geometry there will be no criticality.
- In a nuclear reactor, the fissions occur at a controllable pace due to a number of factors, including the dependence on delayed neutrons to achieve criticality,
- While in a nuclear weapon all of the fissions come from prompt neutrons so the reaction proceeds much more rapidly.